| [191] | Halogen and Chalcogen Binding Dominated by Density-Driven Errors , The Journal of Physical Chemistry Letters 10, 295-301 (2019). |
| [189] | Quantifying Density Errors in DFT , The Journal of Physical Chemistry Letters 9, 6385-6392 (2018). (PMID: 30335392) |
| [180] | Benchmarks and Reliable DFT Results for Spin Gaps of Small Ligand Fe(II) Complexes , Journal of Chemical Theory and Computation 14, 2304-2311 (2018). (PMID: 29614856) |
| [173] | The Importance of Being Inconsistent , Annual Review of Physical Chemistry 68, 555-581 (2017). (PMID: 28463652) |
| [166] | Improved DFT Potential Energy Surfaces via Improved Densities , The Journal of Physical Chemistry Letters 6, 3802-3807 (2015). (PMID: 26722874) |
| [149] | Ions in solution: Density corrected density functional theory (DC-DFT) , The Journal of Chemical Physics 140, 18A528 (2014). |
| [141] | Understanding and reducing errors in density functional calculations , Phys. Rev. Lett. 111, 073003 (2013). [supplementary information] |
| [131] | Communication: Avoiding unbound anions in density functional calculations , J. Chem. Phys. 134, 171103 (2011). |
| [127] | Finding electron affinities with approximate density functionals , Molecular Physics 108, 2687-2701 (2010). |
| [126] | Accuracy of Electron Affinities of Atoms in Approximate Density Functional Theory , J. Phys. Chem. Lett. 1, 2124-2129 (2010). |
Density-Corrected Density Functional Theory
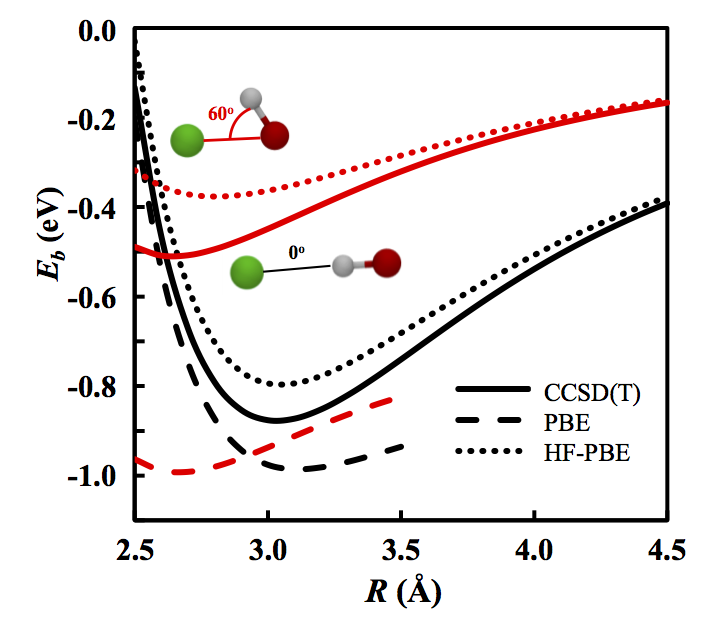
In the early days of DFT, non-self-consistent Kohn-Sham energy was often evaluated upon Hartree-Fock (HF) densities as a way to test new approximations. This method was called HF-DFT. It has been discovered that in some cases, HF-DFT actually gave more accurate answers when compared to self-consistent DFT calculations.
By using a scheme proposed on Ref. 141, we found that DFT calculations can be categorized into two different types of calculations. First we decompose the error of an approximate functional into two parts: error from the functional (functional error), and error from the density (density-driven error). For most calculations, functional error is dominant, and here self-consistent DFT is usually better than non-self consistent DFT on more accurate densities (which we call density corrected DFT (DC-DFT)).
Unlike these 'normal' calculations, there is a class of calculations where the density-driven error is much larger, so DC-DFT give better a result than self-consistent DFT . We classify these calculations as 'abnormal'. HF-DFT is a simple implementation of DC-DFT and we found that a small HOMO-LUMO gap is an indicator of abnormal calculation, thus, HF-DFT would perform better in such cases.
We are trying to determine which are abnormal cases among well-known problematic cases in DFT, and applying DC-DFT to solve these challenging problems.
